Press enter to skip the top menu

Computer Fundamentals

Binary Numbers

Learning Outcomes

On completion of this chapter you will know:

Introduction

5736. When we see this group of digits we instinctively say five thousand, seven hundred and thirty six. We are now so used to interpreting numbers of this type that we do not even think about the rules we use to interpret them. How we interpret them is as follows:

Thus the number 5736 can be broken down as:

5 X 1000 + 7 X 100 + 3 X 10 + 6

How did people hit on the number ten as a base for their counting?

Since they were able to speak some two million years ago, our ancestors have been counting. At the most basic level a mother had to count how many children she had, a man had to count how many wives he had and in some rare cases a woman had to count how many husbands she had. As human society progressed farmers had to count how many pigs, cows, horses and sheep they had.

Those early people were illiterate, and had no pens or paper anyway, and thus they had to use some other means of being able to memorise how many children, wives, husbands etc that they had. We all have hands with the same number of fingers on each hand – in other words we all come equipped with our own simple computer.

Since we all have ten fingers, ten became the basis of our counting system. In the beginning this was sufficient for counting the number of wives and husbands etc, but as civilization progressed and farming became large scale the fingers of the two hands were no longer sufficient to count the number of workers on the farm, the number of pigs and cows etc. This led to the next leap forward in mathematics.

Once a number reached ten a specially carved stone or block of wood would be used to denote a group of ten. Two blocks meant twenty, three blocks meant thirty and so forth. Thus if a prehistoric farmer wanted to say that he had 86 cows on his farm he would eight carved blocks in front of him then hold up one hand and one finger of the other hand. Of course if he wanted to leave a message in his absence he would leave the eight blocks and with them lay down six sticks which would be more practical than chopping off six of his fingers!

As cities developed, commerce began to keep pace. A merchant now had to deal with very large numbers and counting up to a hundred was no longer sufficient. Thus other different stones or blocks of wood were developed to denote ten groups of ten. In other words we had an object to denote a hundred. It was only a very small step from here to design a third block to denote a thousand, ie ten hundreds.

Along with commerce and mathematics writing also developed. Clearly when making long journeys it was more practical for a merchant to carry paper and a bottle of ink than a bag of heavy stone objects. Thus written symbols for single units ten, hundred and thousand were developed. An example of those symbols and how they were used is as follows: if f means a single unit, a means ten, v a hundred and c a thousand then 5736 could be written as cccccvvvvvvvaaaffffff.

When the Romans developed the modern alphabet over two thousand years ago the following symbols were used:

Single unitI
FiveV
TenX
fiftyL
HundredC
Five HundredD
ThousandM

Using this system the number 5736 was written as MMMMMDCCXXXVI

Normally the Roman numerals have a left to right progression with the largest numbers to the right. Thus MCI is 1101 – we add the numbers represented by the letters. On the other hand if a small letter comes before a large one we subtract the two of them. Thus 9 is written as IX instead of VIIII. Similarly 90 is XC. This is in order to reduce the number of digits that have to be written.

The number system that we use today developed only about one thousand years ago.

Go to top

Bases other then ten

Although the majority of the human race used ten as a base for their counting some races used other bases. Apart from ten, the most common other bases were five and twenty. Five was used by those who used only one hand as a base for counting while twenty was used by those who used both their fingers and their toes for counting. Within the different cultures of Papua New Guinea both five and ten are used as bases.

In Konowa, the language spoken by the Tolai people of the East New Britain province, the counting numbers are: tikai, aurua, autul, aivat, ailima, laptikai, lavurua, lavutul, lavuvat, avinun. Clearly the Tolai people used five as their base, since the words for six, seven eight and nine are the same as those for one to four except that la or lap replace the au.

In Europe base twenty was at one time as common as base ten. In the French language traces of this can still be seen. French has no word for seventy, eighty or ninety. A French person will use soixante-dix for seventy, which literally means sixty and ten. The same person will say quatre-vingt for eighty which means four twenties.

In English twenty was called a score. An old English folk song lamenting fishermen who were lost in a storm begins:

Three score and ten boys and men

Were lost from Grimsby town.

From the first two lines of this song we can deduce the sad fact that seventy fishermen from Grimsby were drowned.

Got to top

Base 5

Since we mentioned it above let us look at how numbers would be represented using base 5. Before we do, however let us look more closely at the base of ten. Some observations we have to make are:

Applying those observations to base five we have:

If we have the number 2431 as a base five number we convert it to base ten as follows:

Fig 1

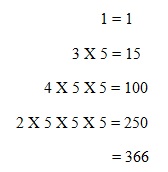
Conversely we can convert a base ten number to base 5 by continuous division by 5. The remainders will be the digits of the new number. Thus to convert the base ten number 2486 to base 5 we proceed as follows:

Fig 2

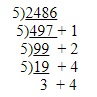
Now starting from the bottom we write out the remainders as follows: 34421 base 5. If we were to convert this number back to base ten again we would find that the result would be 2486 base ten.

As with base five a base seven number would have digits 0, 1, 2, 3, 4, 5, 6. Thus the number 435 base 7 would be equivalent to

Fig 3

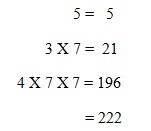
Similarly converting 222 back to base seven by continuous division by seven would yield 435 base 7.

All other bases work in exactly the same way, but we shall examine two special bases, base 2 and base 16, or binary and hexadecimal numbers as they are called.

Got to top

Binary Numbers

Conversion between bases

Binary numbers are numbers to the base 2. Following the rule for other bases, this means that we have digits up to but not including the base itself. That means that the digits for base 2 are 0 and 1. For this reason a binary number would look as follows: 1101011

To convert this number to base 10 we follow the same rules as we did for other bases.

Fig 4

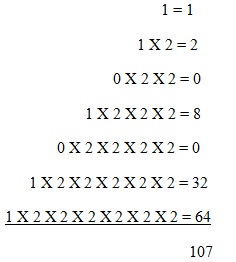
Again this base ten number, 107, can be converted back to binary with continuous division by 2 as follows:

Fig 5

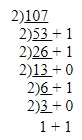
Addition of Binary Numbers

Binary number can be added just as numbers in other bases can be added. The main rules for addition of binary numbers is as follows: 0 + 0 = 0; 0 + 1 = 1; 1 + 0 = 1; 1 + 1 = 10. to people used to the base ten numbers the last rule looks odd at first glance, but remember that in binary numbers our normal number two is written as 10. Following the above rules we can perform the following additions:

Fig 6

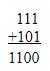
Let us explain this, starting at the rightmost digits. Here we follow the rule 1 + 1 = 10. Thus, following normal addition rules we put down the zero and carry the one. This is carried to the middle pair of digits. We add it to the bottom digit which is zero. Thus 1 + 0 = 1. Now we add this result to the top digit which is 1. Thus 1 + 1 = 10. Again we put down the zero and carry the one. This time we carry it to the leftmost pair of digits. We add our carried one to the bottom digit i.e. 1 + 1 = 10. Finally we add this result to the top digit i.e. 10 + 1 = 11.

Subtracting binary numbers

Although the addition of binary numbers follows the same rules as addition in any other base, subtraction of binary numbers differ from our base 10 subtraction rules. In order to subtract two binary numbers we perform a 2’s compliment on the second number. 2’s compliment means:

  1. Change all the 1’s to zeros and the 0’s to ones
  2. Add 1 to the result

Let us give an example of this form of subtraction. If we wish to perform the subtraction 110110 – 101111 we have to first do a 2’s compliment on the second number.

The first stage i.e. reversing the ones and zeros gives us 010000.

We add 1 to this value which gives us 010001

Now we add this to the first number as follows:

Fig 7

Here the two numbers we were subtracting were six digit numbers. Once we added one of them to the 2’s compliment of the other a final carry resulted in a seven digit number. We ignore this carry which means that the result of our addition of the 2’s compliment is 000111.

In order to double check that this very strange form of subtraction actually works we can convert the three numbers in question to base ten and check that the third number is the difference between the other two.

The first number – 110110 - converts as follows 0 + 2 + 4 + 0 + 16 + 32 = 54.

The second number - 101111 – converts as 1 + 2 + 4 + 8 + 0 + 32 = 47.

The result of the subtraction – 000111 – converts as 1 + 2 + 4 = 7.

Since 54 – 47 =7 we know that the 2’s compliment system has worked correctly.

Before leaving binary subtraction we shall look at one more example. Here we shall perform the following subtraction: 110111 – 101. This time we notice that the two numbers have a different number of digits. In order for the 2’s compliment to work correctly the two numbers must have equal number of digits. For this reason we must pad out the second number – 101 – with extra zeros so that it will look like 000101. Reversing the ones and zeros here will give us 111010. Adding 1 to this gives us 111011. Now we perform our addition on those two numbers.

Fig 8

Once again we can double check our subtraction by converting the three numbers to base ten and checking that the third number is the difference between the first two.

110111 converts as 1 + 2 + 4 + 0 + 16 + 32 = 55

101 converts as 1 + 0 + 4 = 5.

110010 converts as 0 + 2 + 0 + 0 + 16 + 32 = 50

Again since 55 – 5 = 50 we can presume that the 2’s compliment works correctly.

Got to top

Hexadecimal numbers

Basics

Hexadecimal numbers or numbers to the base of sixteen are at the opposite end of the scale to the binary numbers. Whereas the binary numbers use only two of our ten numeric digits, we don’t even have enough digits to represent the hexadecimal numbers. For this reason we have to use alphabetical characters to represent the upper range of the hexadecimals.

Remember that in any number base we must have symbols for all of the numbers up but not including the base. With numbers in the base sixteen we must have symbols for all of the numbers up as far as fifteen. Due to the predominance of base 10 we have symbols up as far as nine. For this reason we must use alphabetical characters to represent the numbers ten to fifteen. Thus ten is represented by A, eleven by B, twelve by C, thirteen by D, fourteen by E and fifteen by F.

An example of hexadecimal number would be 5AF. We would convert this number to base ten in exactly the same way as we would convert numbers in any other base:

Fig 9

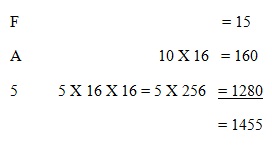
Before moving on we shall look at one more example of converting a hexadecimal number back to base ten, this time the number C2E.

Fig 10

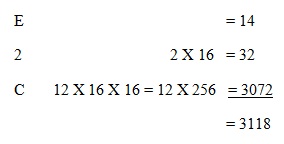
Converting between binary and hexadecimal

You may wonder why use such an unwieldy base as 16. After all if it goes into four digits or more converting it to base ten can be difficult and requires at least a calculator. Firstly it is never intended to be converted back to base ten as it is never used for non computing purposes. The main reason for its use is that, as you will find out in the next chapter, internally computers can only process binary numbers. For the human user, however keying in long strings of 1’s and 0’s is likely to be error prone and tedious. Double checking the same binary numbers is equally error prone and tedious.

For this reason humans never key in binary numbers directly. Instead they are first converted to hexadecimal and then the hexadecimal version is keyed in. Converting between those two bases is very easy. As an example of the conversion we shall look at the first hexadecimal number we worked with above – 5AF.

This number converted to 1455 base ten. If we convert this number to binary we will get 10110101111 base 2. As we have just said keying a number such as this in manually is likely to be error prone and so we shall convert it to hexadecimal. To do this we break it into groups of four digits starting from the right as follows:

101 | 1010 | 1111

The first group – 101 – converts as follows: 1 + 0 X 2 + 1 X 4 = 1 + 4 = 5.

The middle group – 1010 - converts as 0 + 1 X 2 + 0 X 4 + 1 X 8 = 2 + 8 = 10. In hexadecimal this is A.

The rightmost group – 1111 – converts as 1 + 1 X 2 + 1 X 4 + 1 X 8 = 1 + 2 + 4 + 8 = 15. In hexadecimal this is F.

It is much faster and much less error prone to key in 5AF than a long string of ones and zeros.

Got to top

Exercises

Exercise 1

  1. Why did the majority of the human race use ten as the base for their counting?
  2. As well as ten what other common bases have they used and why?
  3. If a person is four score and ten, how old is he or she?
  4. If a farmer has two hundred and four score heads of cattle, how many animals has he got?

Exercise 2

Convert the following base ten numbers to base 5.

  1. 1324
  2. 3418
  3. 5426
  4. 7209
  5. 12213
  6. 1234
  7. 1809
  8. 4708
  9. 3758
  10. 3759
  11. 2224
  12. 2223

Exercise 3

Convert the numbers in Exercise 2 to base seven.

Exercise 4

Convert the numbers in Exercise 2 to binary

Exercise 5

Convert the following binary numbers to base 10.

  1. 10
  2. 11
  3. 100
  4. 101
  5. 1011
  6. 1100
  7. 110111
  8. 4708
  9. 100000
  10. 100011
  11. 101010
  12. 100110

Exercise 6

Add the following pairs of binary numbers..

  1. 11011 and 11101
  2. 10101 and 111
  3. 10111 and 1011
  4. 11011 and 11011
  5. 11110 and 10001
  6. 100011 and 111100
  7. 111011 and 101110
  8. 10101 and 110110
  9. 1110011 and 1111001
  10. 100011 and 101010
  11. 101010 and 111100
  12. 100110 and 11011

Exercise 7

Using 2’s compliment, subtract the following pairs of binary numbers..

  1. 111000 and 1011111
  2. 101010 and 100
  3. 111000 and 11111
  4. 110011 and 101010
  5. 110011 and 101
  6. 110111 and 110110
  7. 111110 and 11111/li>
  8. 111110 and 10000
  9. 1011 and 1010

Exercise 8

Convert the following hexadecimal numbers to base ten.

  1. CAD
  2. FAB0
  3. FAD
  4. A45
  5. C56
  6. 123
  7. 56F/li>
  8. AD4

Exercise 8

Convert the following hexadecimal numbers to base ten.

  1. CAD
  2. FAB0
  3. FAD
  4. A45
  5. C56
  6. 123
  7. 56F/li>
  8. AD4

Got to top